The conventional four-valve systemdescribed previously is pretty good except for the 6th, 7th, and 9-11 semitones. We can solve at least one of those "problem" notes by adding a 5th valve.

We could make the 5th valve tubing long enough to play that problem note using the 5th valve alone, OR we could use the 5th in combination with one or more of the other valves. There are 16 possible combinations that we could choose, so there are 16 possible tubing lengths that we could choose for the 5th valve that will solve that particular problem note. For each of those 16 possibilities we could figure out a fingering chart for the rest of the scale, using the 5th valve wherever it turns out to be helpful. Since there are five major problem notes in the list above, it seems that there are 80 different fingering charts that need to be considered.

Perhaps it would be foolish to make the 5th tubing so long that it can be used only for the 9th, 10th, or 11th semitone. If we are going to have a 5th valve then we should plan to use it more than once a year. So let's plan to use it mainly for the 6th and 7th semitones and hope that it will turn out to be useful for the other problem notes as well. That leaves us with only 32 possible choices.

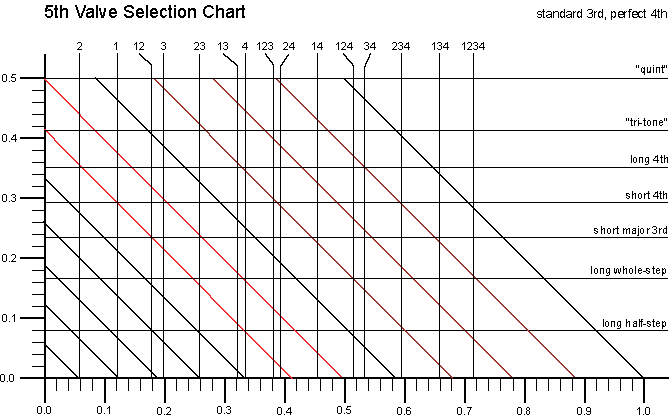
A graphical shortcut enables us to shorten the list of choices considerably. Although not as precise as a spreadsheet, this method makes multi-valve fingerings easy to see and understand. Of course one must remember that real tubas have individual quirks of intonation which cause them to differ from the mathematical model described here. This model is only a starting point for understanding your instrument. It is also very useful for discovering alternate fingerings.

Here is my reasoning: (If you don't like mathematics you can skip down to the next section below to see the results.) Let "T" represent the amount of valve tubing needed to play a "problem note". If we choose to make the problem note playable with the 5th valve alone, then its length must be equal to T. But we could also make the 5th valve tubing shorter and make up the difference by using some of the other valves. Let “Y” represent the 5th valve tubing length, and let "X" represent the tubing length contributed by the other valves. Then Y + X = T, or Y = T - X.

The graph of this equation is a straight line with negative slope, intersecting the axes at X = T and at Y = T. There is one such diagonal line for each note of the chromatic scale, because each note has its own "T" value. For now we need to consider only the ones corresponding to "problem" notes. They are drawn in red in Mark Wiseman's excellent version of the graph, below. The horizontal and vertical axes of this graph are calibrated as decimal fractions of the horn's overall effective length, or "Lo".

Although "Y" (the 5th valve tubing length) can have any value that we choose, there are only 16 discrete values for X. They are 0, L₂, L₁, L₁₂, L₃, L₂₃, L₁₃, L₄, L₁₂₃, L₂₄, L₁₄, L₁₂₄, L₃₄, L₂₃₄, L₁₃₄, and L₁₂₃₄. ("L₂" represents the length of the second-valve tubing, "L₁" is the first, "L₁₂" represents the sum of L₁ and L₂, etc.) Vertical lines are drawn from each of those points on the horizontal (X) axis. For example, the vertical line labeled (23) hits the X-axis at 0.126, because the tubing length of valves 2 & 3 together is conventionally 0.126 Lo. (That's because valves 2 & 3 together are normally used to lower the pitch by a major third, or five semitones, and S to the 5th power is about 1.126.) Naturally, if you like to use different lengths for your valve tubing, then the positions of those vertical lines must be altered. That's easy to do if you use a drawing program on a computer, since you can click on a line and drag it to any position that you like.

The diagonal lines originate from points on the X-axis which correspond to notes in the equal-tempered chromatic scale. For example, the diagonal labeled "T6" originates from 0.414 on the Y-axis and ends at 0.414 on the X-axis, because the valve tubing length needed for the sixth semitone (augmented 4th) is S⁶ × Lo - Lo, which comes out to approximately 0.414 Lo.

Next, the places where a diagonal line and a vertical line intersect are circled, as in the diagram below. They tell us what fifth-valve tubing lengths can be useful. If the intersection point is slightly above the horizontal line then that particular fingering will theoretically be a bit sharp, because pulling the 5th valve slide is equivalent to raising the horizontal line. If the intersection point is below the horizontal line then that fingering is expected to be flat.

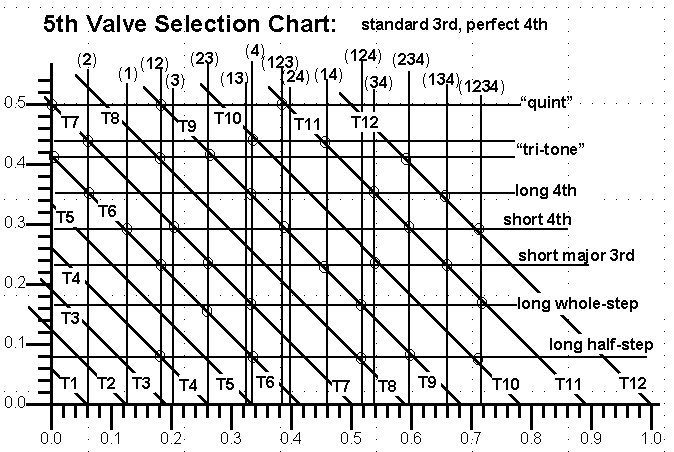
Example 1: Look at the place where the vertical line labeled "(4)" intersects the horizontal line labeled "T6". The height of that spot above the X-axis is approximately 0.0794 Lo, because S⁶ - S⁵ = 0.0794. (Remember that "S" represents the "semitone ratio", or the 12th root of 2.) That turns out to be about one and one-third times the length of the second-valve tubing, or "1.33 L₂". (This is the fifth valve that was invented and patented in 1835 by Wieprecht and Moritz.) Using that length for your 5th valve tubing enables you to get a good 6th semitone (augmented 4th) fingered with the 4th & 5th valves. Furthermore, if you follow the horizontal line labeled “long half-step” to the right from that point you find another circled point where the “T9” diagonal intersects the "(234)" vertical. That tells you that the same 5th valve tubing with valves 2, 3, & 4 will give you an accurate 9th semitone. We see that a "long semitone fifth valve" is good for the 6th and 9th semitones and may be usable for the 10th, but not much help for the other problem notes such as the 7th, 11th and 12th semitones. This system may also be useful for creating alternate fingerings to deal with high notes that have intonation problems. Using "+" to indicate a needed slide pull and "-" to indicate a needed slide push, the chromatic scale then looks like this:

Interval................Fingering..................Note Names

0 (open)....................open....................Bb.....C......Eb.....F

1 semitone...................2.......................A.......B......D.......E

2 semitones.................1.......................Ab.....Bb....Db.....Eb

3 (minor 3rd)..............12(+)..................G.......A......C.......D

4 (major 3rd)..........23/125...................Gb.....Ab.....B......Db

5 (perfect 4th).............4........................F.......G......Bb.....C

6 (tritone)...................45.......................E......Gb.....A.......B

7 (imperfect 5th).......124(--)..................Eb.....F......Ab.....Bb

7 (imperfect 5th).......245(++)................Eb.....F......Ab.....Bb

8 (augmented 5th)....234(-)....................D.......E......G.......A

9 (sixth)...................2345.....................Db.....Eb....Gb.....Ab

10 (seventh)............12345(-).................C.......D.......F.......G

11 (major seventh)...NA........................B.......Db....E......Gb

(The four columns under "note names" are for instruments in keys of BBb, CC, Eb, and F, respectively.)

Notice that the 4th semitone in this system can be fingered 125 instead of 23. One could take advantage of that coincidence by shortening the T3 length to use the 3rd valve instead of 12. That possibility will be explored later with another diagram and fingering chart for short third-valve systems.

Example 2: The horizontal line labeled "long whole-step" hits the vertical (y) axis at roughly 0.165 Lo, which comes out to roughly 2.7 L₂. (Tuning the 5th valve to give a perfect 5th fingered 45 makes T5 = S⁷ - S⁵.) It has marked intersection points on diagonals T6, T7, T9, and Tll, showing that it comes reasonably close to solving those four problem notes, but is not much help on T10, and does not give us any alternate fingering for the pedal note, T12. The chromatic scale looks like this:

(Again, the four columns under "note names" are for instruments in keys of BBb, CC, Eb, and F, respectively.)

The signs in parentheses indicate that some lipping or slide adjustment will be needed. A plus sign means a small amount of slide pull may be needed; a double plus sign indicates an adjustment of more than ten cents will be needed.

If you tune the 5th valve for the 7th semitone fingered 45 (as in the chart above) then the sixth semitone will be a bit flat when fingered 235. Shortening the third valve tubing a bit will partially correct that problem, leaving the 23 combination a bit sharp. The chart suggests that you could also tune the 5th valve for the 6th semitone fingered 235, but then the 7th, 9th and 11th semitones would be a bit sharp. That might be acceptable because it’s usually easier to lip down than up in the extreme low register. Again, this type of 5th valve may give many alternate fingerings for correcting intonation of problem notes in the high register. More discussion of that subject will appear later.

Example 3:
The next horizontal line is labeled "short major 3rd", sometimes known as the "Mirafone System" or "two whole-step". It hits the Y-axis at roughly 0.2323 Lo, or about 3.9 L₂. If we tune the 6th semitone fingered 125 then

I suspect that Fred Geib may have invented this popular system. The oldest tuba I have seen that used this system was originally his. (Actually, on his tubas the order of the 4th and 5th valves was reversed; his 4th valve was two whole-steps, and his fifth valve was a perfect fourth.) Again,we find good fingerings for T6, T7, T9, and T11, but not T10 or T12. The intersection points seem to line up a little better than in example 2, suggesting that the intonation may be slightly better with this system. The fingering chart looks like this:

(Standard third valve, Perfect fourth valve (slightly sharp so that 234 and 145
are only slightly flat, Fifth valve = short major 3rd set for 125 = tritone)

Because of the length of tubing involved, this type of 5th valve will be somewhat less useful for alternate fingerings in the upper register. But it does give an unusually good extension register, with the eighth and ninth semitones only a tiny bit flat and a sharp but usable alternative to the pedal note.

Example 4: ("Short 4th") This unusual 5th valve has a tubing length of roughly 0.292 Lo, or about 5 times L₂.
Fingering the sixth semitone with 1 & 5 means T5 = (S⁶ - 1)Lo - L₁ = 0.2918 Lo. It gives excellent pitches for all the notes except for the tenth semitone. T12 may be usable as an alternate fingering for the pedal note with some lipping up or slide pushing:

The possibilities and limitations of other 5th-valve systems such as the long fourth, tritone, and quint can also be seen easily on the chart. A fifth valve tuned to a "long 4th" gives you good fingerings for T6, T9, T11, and T12, but is no help for T7, T8, and T10. The Gronitz "tritone" valve offers possible fingerings for every note, but with considerable variations in pitch. A "quint" valve (tuned to a perfect 5th) gives good fingerings for T7, T9, and T11.

More precise calculations are easily performed with a spreadsheet such as my Downloadable Microsoft Excel Spreadsheets. There are actually two spreadsheets in the download, called "sheet 1" and "sheet 2". (You can select one or the other by clicking on little tabs at the lower-left hand corner.) Sheet 1 is for four-valve tubas and sheet 2 is for 5-valve instruments.
Every possible fingering combination is calculated automatically, along with theoretical pitch errors and slide pulls. You can type your own values for the valve tubing lengths into cells B2-F2 (on the 5-valve sheet) and see what happens instantly. (On the four-valve sheet just type over the boldface numbers in column B.) The apparent precision of this method may be misleading because it does not take into account the individual quirks of real instruments. (A tuba is really more complicated than a guitar string.) But if you do find that a certain fingering is not as good as the spreadsheet suggests, you can often find another one that compensates for the quirks of your instrument.

The charts above are based on a fourth valve tuned to a perfect fourth. I prefer that tuning because I can easily pull either the fourth or the second valve slide whenever I use the 2 & 4 combination. As mentioned earlier, Chester Roberts advocated keeping the fourth valve slide pulled out all of the time, which alters the chart significantly and leads to different fingering systems. Roberts Systems:

Another approach which is popular in Europe but strongly opposed by Roberts is to tune the third valve to be used alone as a substitute for 1 & 2. To see an investigation of this system click on "short third valve".